6軸センサー(MPU6050などのIMUセンサー)から、3軸回転を考慮した傾き角度(姿勢角度)の算出方法、補正方法(ジャイロドリフト補正)はいろいろあると思いますが今回は相補フィルターを例に姿勢推定を解説したいと思います。(ここら辺りの内容は散発して記事を投稿していたのですが、一度纏めたいと思います)
概要
6軸センサーではジャイロ(3軸角速度)、加速度センサー(3軸加速度)の値を取得できます。ジャイロのみでも加速度センサーのみでも角度算出はできるのですが、センサー毎に特徴がありその特徴を補う形で補正を行い、より正確な姿勢角を導きます。
▼姿勢算出をビジュアルで確認▼
▲カルマンフィルターが少し変な動きしてますが、カルマンフィルターが悪いのでなく、使用した言語ライブラリ(プログラム)が悪いだけです。後述しますがカルマンフィルターライブラリ内部の角度計算がベクトル回転を考慮していないためです。
センサー値の補正には便利なフィルター、カルマンフィルターやMadgwickフィルターなどがあります。言語ライブラリも存在し使用するだけなら比較的簡単なのですが数学的理解が私とっては難解。ブラックボックス的なものはあまり使用したくないということもあるので、今回は感覚的にも理解しやすい相補フィルターを使って姿勢角度を推定していきます。
考え方はとしては、ジャイロ値のみで加速度ベクトルを更新。更新したベクトルは加速度センサー値のベクトルと一致するはずでが、センサーにはそれぞれ特性とか誤差とかがあるため一致しません。そのずれを補正して正確な姿勢角度を算出します。
ではまずジャイロ値(角速度)からの角度算出方法とのその特徴です。
ジャイロ(角速度)からの3軸角度算出方法と特徴
MPU-6050の使い方
角速度から角度の算出方法
はそれぞれ別の投稿記事で解説してますのでそちらを参考にして下さい。
ジャイロからの角度算出ですが、センサーから取得した角速度を時間で積分すれば角度となります。1軸回転のみを検出するのであれば単純な積算でも算出できるのですが、3軸回転となると少しややこしくなります。
センサー軸自体が傾いてしまうため、そのベクトル(センサー軸の傾き)を考慮する必要があります。
動画で確認
(わかり難いでしょうか)上図のような回転があった場合、最終的には姿勢角は水平になるはずなのですが(z軸回転のみ残る)、単純に各軸を積算するだけではx軸、y軸ともに角速度からの積算値が残ってしまうため、おかしな算出値になってしまいます。
3軸回転の場合はただの積算ではなく、回転行列や四元数などを使ってベクトルを合わせて算出する必要があります。四元数は私にとっては数学的理解がなかなか難解なので、今回は回転行列を使用して算出してみたいと思います。
軸ベクトルのズレ
まず、センサー系でx軸回転後にz軸回転を加えた場合、x軸の傾きがどのように変わっていくのかを3DCadで作図しながらその角度を測定してみました。
▼3DCadから角度を測定▼
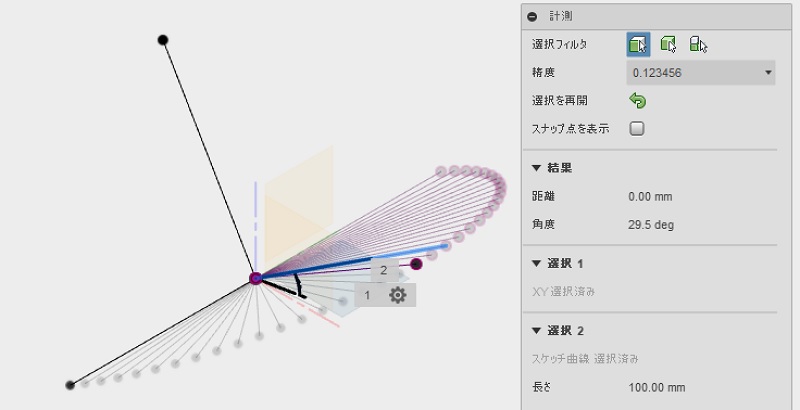
CADで作図しながら少しずつ実角度を測定してます。測定している角度は、x軸廻りに30度回転後(y軸が水平面と30度の状態)でz軸回転を少しずつ加えた時の「水平面」と「x軸」との角度です。
▼z軸回転角度とx軸の傾きの移り変わりをグラフにすると▼
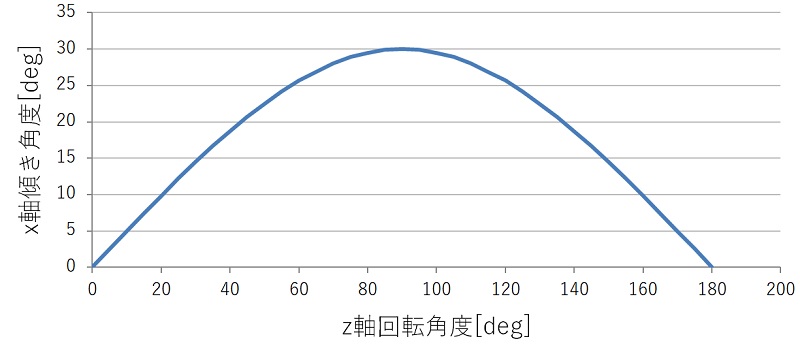
z軸回転に合わせてx軸に傾きが発生します。絶対座標系のZ軸回転であればこういったことは起こりませんが、センサー座標系となるため、ベクトルを気にせずに算出するとこういった現象が起きてしいます。(先ほどの動画、カルマンフィルターのズレはこれが原因です。)
こういったことが起こるため3軸で回転がある場合は、単純な積算ではなく回転行列などで姿勢角度を更新していきます。
ジャイロ値から回転行列でベクトル更新
3次元だとややこしいので2次元(1軸)でみてみます。
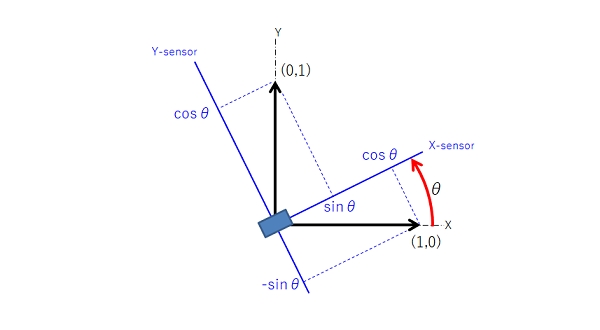
▲単位ベクトルをθ回転後のセンサーから見た場合、座標変換行列から、
\begin{align} \\ \begin{bmatrix}x_x&y_x\\x_y&y_y\end{bmatrix} = \begin{bmatrix} \cos\theta &\sin\theta\\ -\sin\theta &\cos\theta\end{bmatrix}\begin{bmatrix}1&0\\0&1\end{bmatrix} = \begin{bmatrix} \cos\theta &\sin\theta\\ -\sin\theta &\cos\theta \end{bmatrix}\\\\ \end{align}▲回転後のベクトルはこのように計算されます。単位ベクトル掛けてるだけなので展開式としてはあまり意味ないです。回転後のベクトルにまたさらに座標変換を繰り返して、、とジャイロ値を使用して延々とベクトルを更新し続ける要領で姿勢(角度)を把握します。
3次元も同様の考え方で見てみます。
▼左からxyz軸の順での座標変換行列▼
\begin{align}\\ R= \begin{bmatrix} 1 &0 &0\\ 0 &\cos\theta_x &\sin\theta_x\\ 0 &-\sin\theta_x &\cos\theta_x \end{bmatrix} \begin{bmatrix} \cos\theta_y &0 &-\sin\theta_y\\ 0 &1 &0\\ \sin\theta_y &0 &\cos\theta_y \end{bmatrix} \begin{bmatrix} \cos\theta_z &\sin\theta_z &0\\ -\sin\theta_z &\cos\theta_z &0\\ 0 &0 &1 \end{bmatrix} \\\\ \end{align}▲このまま利用してもいいのですが、結構複雑なので少し簡素にします。
センサーで取得するジャイロ値(角速度)は微小な時間間隔でサンプリングを前提として、\(\cos\theta\approx1\)、\(\sin\theta\approx\theta\)と近似、さらに2次項目もほぼ0ということで近似して展開すると、
\begin{align} \\ \Delta R= \begin{bmatrix} 1 &\theta_z &-\theta_y\\ -\theta_z &1 &\theta_x\\ \theta_y &-\theta_x &1 \end{bmatrix} \\\\ \end{align}▲ここまで簡素な式になります。このような近似を無限小回転というようです。回転順に関係なくこの式になります。この式とジャイロ値から算出される角度で各軸ベクトルを更新し続ければ、常に姿勢が把握できることになります。
また回転行列から角度(ベクトルからオイラー角)への変換は
\begin{align} \\ R&= \begin{bmatrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \\ a_{20} & a_{21} & a_{22} \end{bmatrix} \\\\ \end{align}▲ベクトルの各要素をこのように置いたとき、それぞれの角度は、各要素から
\begin{align} \\ \theta_x &= \tan^{-1}\frac{a_{12}}{a_{22}} \\\\ \theta_y &= -\tan^{-1}\left(\frac{{a_{02}}^2}{\sqrt{{a_{12}}^2+{a_{22}}^2}}\right) \\\\ \theta_z &= \tan^{-1}\frac{a_{01}}{a_{00}} \end{align}と計算できます。
▼無限小回転の展開や回転行列からオイラー角度の算出はこちら▼
ただ、こういったジャイロからの角度算出(回転計算)には少し欠点があります。
角度算出に積分を使用しているため、センサー誤差やノイズなどをどんどん積算してしまい角度がずれていってしまいます(ジャイロドリフト)。
ジャイロドリフトの確認
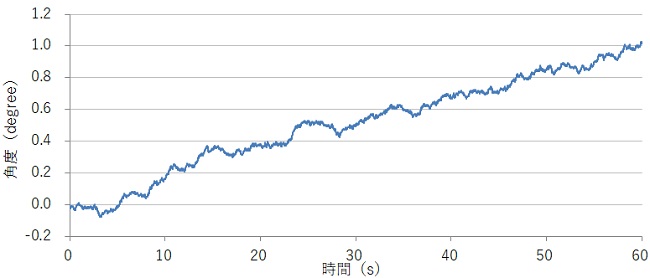
このグラフではジャイロドリフトを確認してます。センサーを水平に置いたまま、ジャイロ値を積算し角度を算出しているのですが、時間が経つにつれて角度が発生します。誤差やノイズなども積算してしまうため発生する現象です。(発生具合は個体差や環境によります。)
このずれ(ジャイロドリフト)を補正する必要があるのですが、補正を行うために加速度センサーの値を使用します。
加速度センサーからの角度算出方法と特徴
加速度センサーからの取得値からの傾き角度ですが
acc[ROLL] = atan2(ay, az) * pi()/180; acc[PITCH] = -atan2(ax, sqrt(ay * ay + az * az)) * pi()/180;
で算出することができます。いろいろと算出方法があると思います。計算の一例です・・・。
▼加速度から角度算出方法はこちら▼
特徴として、加速度センサーからはz軸廻り(yaw回転)の角度は算出は困難。またセンサーの加減速を拾ってしまうため値が結構暴れます。またセンサー自体に加減速がある場合には計算される角度がおかしくなってしまいます。
こういったことを考慮に入れて使用する必要があります。
各センサーからの角度算出まとめ
ジャイロからでも加速度センサーからでも傾き角度(姿勢角度)は算出できるのですが、それぞれの特徴があり、補正を行ってより正確な傾き角度を算出します。
◆ジャイロの場合
- 3軸回転がある場合は単純な積算ではなくベクトルを考慮する必要がある。
- 誤差が蓄積して角度が少しずつずれていく。(ジャイロドリフト)
◆加速度センサーの場合
- z軸廻り(yaw回転)の角度算出が困難(できない?)
- センサーが加減速しているときには正確な角度算出は困難
- ドリフトは無い
- 長期的には有利だが、短期的には不利
それぞれの特徴を映像で確認
左側が加速度センサーのみから角度計算したものです。センサー自体に加減速が加わるとおかしな角度検出となってます。ただ長期的にはジャイロのようなドリフトは発生しません。
右側がジャイロのみから角度算出したものです。この映像では各軸の単純な積算で角度を計算しています(ベクトルのズレを考慮していない)。ですのでz軸に回転が加わると角度(ベクトル)がずれてしまいます。またさらにドリフト補正も行っていないため、誤差が積み上がりどんどん角度がおかしくなります。ただセンサー自体の加減速の影響は受けていません。
ドリフト補正方法
ここで2つのセンサーから、より正確な角度を算出するための補正を行います。基本的にはジャイロで角度算出し、加速度センサーでジャイロドリフトを補正する方法です。
補正ベクトル = (1-k) * ジャイロからの推定ベクトル + k * 加速度センサーからの検出ベクトル
相補フィルター(簡易的?)です。ジャイロから推定した加速度(重力)ベクトルをそのまま加速度センサーで検出するベクトルで補正します。補正されたベクトルを元にまた次の姿勢を推定して、、、と繰り返します。
加重平均をとっているような(いいとこ取り?)みたいな感じ、加速度センサー側の値を小さくすればするほど微細な動きの影響は無視できますが、補正が遅くなる感じでしょうか。ジャイロ、加速度のどっちに重みを持たせるかってとこでしょうか。
また、ジャイロ+加速度だけではz成分(重力ベクトル)しか補正できないので、z軸回転については補正できません。徐々にドリフトが発生しズレてしまいます。z軸回転も補正するなら地磁気センサーなど組み合わせる必要があります。
ドリフト補正の確認動画
いろいろな方法で角度算出したものを比較してみました。
▼確認動画▼
左から順に、加速度センサーのみ。ジャイロのみ。相補フィルター(本記事で紹介した方法)。madgwickフィルターとなってます。(動画がコマ落ちしてますがすみません)
加速度センサーはz軸(yaw回転)回転は可視化してません。動画途中でセンサーを揺すってますが、加減速が発生すると角度がおかしくなってます。
ジャイロのみからの角度算出は割といい感じで姿勢角を算出できてますが、動画最後にはドリフトが発生していて、水平に戻っていません(少しわかり難いですが)。
簡易相補フィルター、本記事で紹介した方法です。少し加速度の重みが強く少し補正が遅れている感じです。
madgwickフィルターは特に問題なく角度算出している感じです。
長文となってしまいました。ここまで読んで頂きなんですが特にこだわりがなければ、言語ライブラリとかよく公開されているのでそれを使った方が楽かと思います。
▼今回紹介した算出モデルを応用した、モデル、回路(ソースコード)、を頒布してます▼
▼今回の姿勢算出を応用した工作記事はこちら▼




コメント
はじめまして。
ジャイロセンサの勉強を行っているものなのですが、
角度の検出には角速度のみでは誤差が多いことをこちらのブログを拝見して初めて知り、目から鱗です。
1つお願いがあるのですが、madwickフィルターを用いた角度検出のソースコードを教えて下さることは可能でしょうか。
急なお願いで申し訳ありませんが、宜しくお願い致します。
あんぱんさん、はじめまして。コメント有難うございます。
ソースコードを教えることはなかなか難しく困ってしまいます。また私もmadgwickフィルターの中身はほとんどわかっていないためライブラリを使用しているだけとなります。もしArduinoをお使いでしたらライブラリがあるため確認頂いて、そのうえで具体的に質問頂けないでしょうか
記事を拝見させていただき、非常に参考になりました。ありがとうございます。1つ質問があるのですが、
加速度センサーからはyaw回転の角度算出が困難であるとのことですが、確認動画の結果においてはyaw回転についても相補フィルターを通しているように思います。
yaw回転の相補フィルターの式はどのようなものでしょうか?教えて頂けると幸いです。
匿名さん、こんにちは。コメント有難うございます。
yaw回転の補正は残念ながら行っておりません。本ページにある動画の相補フィルターではジャイロ値を積算した値を使用してます。但し、センサー座標系と絶対座標系(ベクトルのずれ)は考慮して角度計算はしてます。動画内ではyaw回転のドリフトがたまたま目に見える程発生していないだけだと思います。
いつもかなりお世話になっております。
ありがとうございます。
ひとつ気になったのでコメントさせていただきます。
角度算出するときに、pi()/180をかけられていますが、
そうすると単位は[rad]になると思いました。
しかし表の縦軸は[degree]表記です。
やはりdegree換算で正しいのでしょうか。
恥ずかしいコメントで申し訳ないです。
返信いただけたら幸いです。
Kokiiさん、サイト拝見下さり有難うございます。
ご質問の件ですが、ご認識いただいている通りです。
この手の三角関数計算は[rad]単位が一般的のため、計算式は[rad]換算してます。
グラフは[deg]のが馴染みやすいため[deg]で表記しているだけです。
かえって紛らわしかったですかね・・。
はじめまして
興味深く記事を拝見してます
自分は今台車にこの6軸センサを付けていまして、傾斜角度に合わせてモーターの回転速度を変えようとしているのですが、台車が動いている時センサーの値が安定しないのですが、これは角度の計算の仕方がよくないからですか?madgwickフィルターを掛けているのですが、何か使い方を間違えているのですかね?
よろしければご返事お願いします
ttさん、サイト拝見くださり有難う御座います。
原因はいろいろ考えられるかと・・、
加速度センサは動きの変化に弱いので加速度の重みを減らすとか
もしくは電気的ノイズを回路が拾ってしまってるとか
ひとつずつ確認していくことが近道かとおもいます。
安定しない=ノイズ的なものではなく、値がずれているようなものであれば計算の仕方かも。
とても分かりやすいMPU-6050で色々とやろうとしているものです.
中々に興味深い記事で勉強になりました.
端的に質問させて頂きます.
「ジャイロドリフト」という単語で私が混乱しているのかもしれませんが,
・ジャイロの値を使って”姿勢角を出す際に”ドリフトが発生する.
・ジャイロの値を使って姿勢角を計算する際の積算の過程において”誤差の積算もしてしまうために”ドリフトが発生する.
という理解で良いのでしょうか?
単にジャイロの各軸で得られる値を個別利用する際には,積算する訳ではないのでドリフトを気にする必要がないと思って良いのでしょうか?
「ジャイロドリフト」と聞くと,ジャイロそのものに問題があるように思えてしまいます.
サイト拝見下さり有難うございます。独学なのでほんとのところはよくわかってませんが、私もジャイロそのものに問題があるのではなく、角度算出に積分を行っているため、その計算方法(積算)により発生する誤差と認識してます。徐々に真値からずれていくものと認識してますでジャイロ値をそのまま角速度(rad/s)として利用する場合や、短期的な角度算出であればドリフト誤差は発生せず、単にずれは測定誤差(精度)と考えていいと思います。
ご回答頂きありがとうございます.
ジャイロ値をそのまま角速度(rad/s)として利用する分には,問題無さそうですし,ジャイロ値を使って色々とやってみたいと思います.
imoさんの記事「Arduinoから MPU6050の値を取得してみる」
で,新たに質問させて頂いたのでご回答いただけると幸いです.
Gyro設定におけるFS_SEL,加速度設定におけるAFS_SEL,LPF設定の43[Hz]はどのようにして調整するのかを教えて頂きたいです.
(「アドレス」や「レジスタ」などがよく分からないので.)
新たな質問が送信されていないようです。
以前の質問は自身で解決しました.
それとは別に質問があります.
ローパスフィルタのレジスタマップの読み方についてです.
「Arduinoから MPU6050の値を取得してみる」の記事で,ローパスフィルタの設定をしておられましたよね?
ここで質問です.
表示していたレジスタマップによると,DLPF_CFG1〜6ではジャイロセンサのFs(kHz)が1になる.というように書いてありますが,これは,「ローパスフィルタを使用するとジャイロセンサのサンプリング周波数が1kHzになると思って良いんですか?」
いつもサイト拝見下さり有難うございます。
私もその認識でいいかと考えてます。
もう一つ質問させてください.
「Arduinoから MPU6050の値を取得してみる」の記事の後半の”ソース全体”で,ローパスフィルタの設定アドレスを[0x05]にしてありますが,この場合も角速度のサンプリング周波数は1kHzになるんでしょうか?
レジスタマップのbandwidth,delayが何を意味しているのか分かりません.
ご存じでしたらご教授願います.
いつもサイト拝見下さり有難う御座います。
1KHzになると思います。(詳細はデータシート確認下さい)
また、帯域幅、立ち上がり時間のことかと思います。
できれば、今後は内容に合わせてその投稿ページにてコメントを頂けますでしょうか。
MPU6050を学習しているものです。いつもご丁寧に説明してくださりありがとうございます。
Processingで可視化していると思いますが、コードを教えていただけないでしょうか。
Ardiunoで相補フィルタや加速度センサ、ジャイロセンサで測定はできているのですが、なかなかProcessingで可視化できずに困っております。
AOさん、サイト拝見下さり有難う御座います。
ソースコードの説明は中々難しく、もし宜しければこちらで頒布しておりますのでご確認頂けますでしょうか。
Arduino、Processingともにソースも同梱されてます。内容は似ているので参考にはなると思います。
https://garchiving.booth.pm/items/3694699