加速度センサーから軸廻り角度への変換計算

　ジャイロ値のドリフト補正を行うため、加速度センサーからの回転角度への計算方法を調べました。いろいろ算出方法があるようですが、調べた内容をまとめておきます。

1軸回転の場合

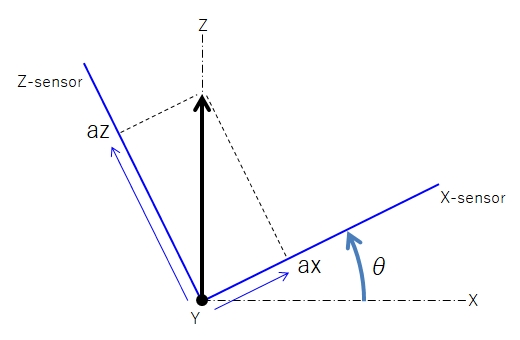
▲上図のように、絶対座標系をx-z平面で見て、y軸廻り（pitch角）にθ回転しているセンサーを考えます。検出される加速度をセンサー座標系（加速度センサー）の ax、az としてます。

　重力方向をz軸としているのでxz平面で図示してます。回転方向やベクトルの向き等で符号（±）は反転するので使用するセンサーに合わせて適宜調整してください。

　算出方法です。1軸回転は単純な三角関数で計算可能。上図からy軸廻り（pitch）の回転角度は三角関数より、

\begin{align} pitch=\cos^{-1}(az)\\ \end{align}

　もしくは

\begin{align} pitch=\sin^{-1}(ax)\\ \end{align}

　で算出可能です。

　ただこれだと検出角度の範囲によって、加速度センサーの分解能の影響が出てしまいます。そこで式を少しいじって、

\begin{align} pitch=\tan^{-1}\left(\frac{ax}{az}\right)\\ \end{align}

　このようにtanが使えるよう変形してます。

　またtan では検出範囲が -π/2<Θ<π/2 になってしまうので言語関数では atan2 関数を使用します。atan2 関数では -π<Θ<π の範囲で計算が可能でし、分母が0でも行けたはず。例えば上記の場合、atan2（az,ax）というような感じです。

3軸（2軸）回転の場合（水平面に対する任意の傾き）

　ここからが本題です。加速度センサーを1軸回転（平面上の回転）のような使い方をするのであれば上記の計算方法で良いかと思いますが、水平面に対する任意の傾きがある場合の計算方法を考えたいと思います。

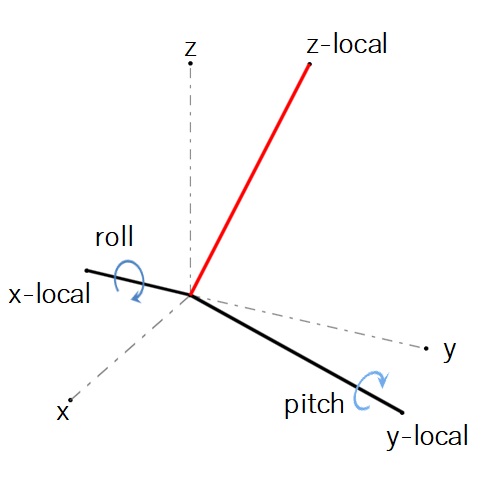
　1軸回転の場合は単純でしたが、3軸（2軸）回転となると少しややこしいです。回転行列（ベクトル）で考えてみます。

絶対座標系で検出する重力ベクトルを常にZ方向として \(\begin{bmatrix}0&0&g\end{bmatrix}^T\) とおきます。またセンサー座標系で検出される加速度ベクトルを \(\begin{bmatrix}ax&ay&az\end{bmatrix}^T\) とします。座標変換の式から以下のようにおいて展開していきます。 \begin{align} \begin{bmatrix}ax\\ay\\az\end{bmatrix} &= \begin{bmatrix} 1 &0 &0\\ 0 &\cos\theta_x &\sin\theta_x\\ 0 &-\sin\theta_x &\cos\theta_x \end{bmatrix} \begin{bmatrix} \cos\theta_y &0 &-\sin\theta_y\\ 0 &1 &0\\ \sin\theta_y &0 &\cos\theta_y \end{bmatrix} \begin{bmatrix} \cos\theta_z &\sin\theta_z &0\\ -\sin\theta_z &\cos\theta_z &0\\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} 0\\ 0\\ g \end{bmatrix} \\\\ &= \begin{bmatrix} C_y C_z &C_y S_z &-S_y\\ S_x S_y C_z – C_x S_z &C_x C_z + S_x S_y S_z &S_x C_y\\ C_x S_y C_z + S_x S_z &C_x S_y S_z – S_x C_z &C_x C_y \end{bmatrix} \begin{bmatrix} 0\\ 0\\ g \end{bmatrix} \\\\ &= \begin{bmatrix} -g\sin\theta_y\\ g\sin\theta_x\cos\theta_y\\ g\cos\theta_x\cos\theta_y \end{bmatrix}\\\\ \end{align}

　回転順で展開式が変わりますが、（絶対座標の）z軸回転をしても重力ベクトルに変化が無いため（センサーの向きが変わるだけ）であまり意味がありません。z軸回転は無い物（もしくは0°）として他のパターンの展開式（回転順）を見ても成分は違えど同様の展開式となります。

　で展開した行列式から、各軸の回転角度を導くように式を整理していきます。

\begin{align} \frac{ay}{az} &= \frac{\sin\theta_x\cos\theta_y}{\cos\theta_x\cos\theta_y}\\\\ &= \frac{\sin\theta_x}{\cos\theta_x}\\\\ &= \tan\theta_x\\\\ \theta_x &= \tan^{-1}\frac{ay}{az} \end{align}

　座標変換の公式をこのように整理していくと、加速度値から x軸回転（roll角）が算出できます。

　さらに、y軸回転（pitch角）については

\begin{align} ay^2+az^2 & = \sin^2\theta_x\cos^2\theta_y + \cos^2\theta_x\cos^2\theta_y\\\\ &=\cos^2\theta_y\left(\sin^2\theta_x + \cos^2\theta_x\right)\\\\ &=\cos^2\theta_y\\\\ \sqrt{ay^2 + az^2} &= \cos\theta_y\\\\ \frac{a_x}{\sqrt{ay^2 + az^2}} &= -\frac{\sin\theta_y}{\cos\theta_y}\\\\ &= -\tan\theta_y\\\\ \theta_y &= -\tan^{-1}\left(\frac{a_x}{\sqrt{ay^2 + az^2}}\right) \end{align}

このように整理します。4行目の式や、\(-\sin\theta_y\)からでも角度算出できますが、複数（3軸）からの検出値の方が信頼性が高そうなのと atan2言語が使用できるのでこのようにします。

　加速度センサーそのものが動的加速度を伴っている場合、正確な計算はできないため注意が必要です。各加速度の検出値がおおよそ \(\sqrt{ax^2+ay^2+az^2}\fallingdotseq1\) となっているのが前提です。

　さらに加速度センサーからの角度算出ではz軸（yaw軸）廻りの回転角度算出が困難です。。水平状態のz軸回転では重力向きに変化がない（また遠心力でx、y軸に加速度が発生してしまう）ため角度計算おかしくなってしまいます。

　途中間違ってないか心配です・・・。表現がおかしなところがあるかもしれませんがすみません・・・。

角度変換計算の検証

　検証にはArduino/Genuino 101の内蔵6軸センサーを使用してます。加速度センサーが内蔵されているため、基本的には外付け部品無しで検証できるので便利です。

　検証といっても傾き角度を計測するのは困難ですので、Processingを使用してビジュアルで見てみたいと思います。

　水平面に対する傾きを、加速度センサーの値から計算。その変換値をProcessing側でビジュアル化してます。

▼確認の動画です▼

　加速度センサーからの取得値のみで動きを可視化してます。割と正確に加速度から傾き角度の算出ができいるようです。