
6軸センサー(加速度、ジャイロ)などの取得値から角度を計算するときに個人的によく見返す回転行列式をまとめておきます。
四元数に比べると回転行列の方が理解しやすく好みです。ただややこしくて使用するたびに頭を悩ますことがあるのでよく使う式と考え方を覚書でまとめておきます。
3軸の回転行列(座標変換行列)です。左からx、y、z軸廻りの順です。
\begin{align} \\ R&= \begin{bmatrix} 1 &0 &0\\ 0 &\cos\theta_x &\sin\theta_x\\ 0 &-\sin\theta_x &\cos\theta_x \end{bmatrix} \begin{bmatrix} \cos\theta_y &0 &-\sin\theta_y\\ 0 &1 &0\\ \sin\theta_y &0 &\cos\theta_y \end{bmatrix} \begin{bmatrix} \cos\theta_z &\sin\theta_z &0\\ -\sin\theta_z &\cos\theta_z &0\\ 0 &0 &1 \end{bmatrix} \\\\ &= \begin{bmatrix} \cos\theta_y\cos\theta_z &\cos\theta_y\sin\theta_z &-\sin\theta_y \\ \sin\theta_x\sin\theta_y\cos\theta_z – \cos\theta_x\sin\theta_z &\sin\theta_x\sin\theta_y\sin\theta_z + \cos\theta_x\cos\theta_z &\sin\theta_x\cos\theta_y\\ \cos\theta_x\sin\theta_y\cos\theta_z + \sin\theta_x\sin\theta_z &\cos\theta_x\sin\theta_y\sin\theta_z – \sin\theta_x\cos\theta_z &\cos\theta_x\cos\theta_y \end{bmatrix} \\\\ \\\\ \end{align}▲センサー座標系のベクトル(加速度ベクトル)のことを考えてここでは座標変換行列で展開してます。角度がマイナスになるだけなので回転行列のsin符号が逆転しただけです。
このままの展開式を利用してもいいのですが結構複雑になるので簡単にします。センサー値をマイコンなどで微小な時間間隔でサンプリングをすることを前提として、\(\cos\theta\approx1\)、\(\sin\theta\approx\theta\)で近似して展開します。
\begin{align} \\ \Delta R&= \begin{bmatrix} 1 &0 &0\\ 0 &1 &\theta_x\\ 0 &-\theta_x &1 \end{bmatrix} \begin{bmatrix} 1 &0 &-\theta_y\\ 0 &1 &0\\ \theta_y &0 &1 \end{bmatrix} \begin{bmatrix} 1 &\theta_z &0\\ -\theta_z &1 &0\\ 0 &0 &1 \end{bmatrix} \\\\ &= \begin{bmatrix} 1 &0 &-\theta_y\\ \theta_x\theta_y &1 &\theta_x\\ \theta_y &-\theta_x &1 \end{bmatrix} \begin{bmatrix} 1 &\theta_z &0\\ -\theta_z &1 &0\\ 0 &0 &1 \end{bmatrix} \\\\ &= \begin{bmatrix} 1 &\theta_z &-\theta_y\\ \theta_x\theta_y -\theta_z &\theta_x\theta_y\theta_z + 1 &\theta_x\\ \theta_y + \theta_x\theta_z &\theta_y\theta_z – \theta_x &1 \end{bmatrix} \\\\ \end{align}となって、さらに\(\theta\)の掛け算は微小×微小なのでほぼ0ということで、
\begin{align} \\ \Delta R= \begin{bmatrix} 1 &\theta_z &-\theta_y\\ -\theta_z &1 &\theta_x\\ \theta_y &-\theta_x &1 \end{bmatrix} \\\\ \end{align}ここまで簡素になります。この考え方を無限小回転というようで、回転順に関係なくこの式にたどり着きます。この行列式を使ってジャイロ値からの角度でベクトルを更新し続ければ、姿勢が常に把握できるようになります。近似が嫌だということであれば近似する前の展開式を利用してベクトル更新します。
下図のイメージのように加速度ベクトル\(\begin{bmatrix}0&0&1\end{bmatrix}^T\)などをセンサー座標系へ変換すれば、そのまま加速度センサー値となるのでセンサーフュージョン(補正)も割とやりやすくなります。
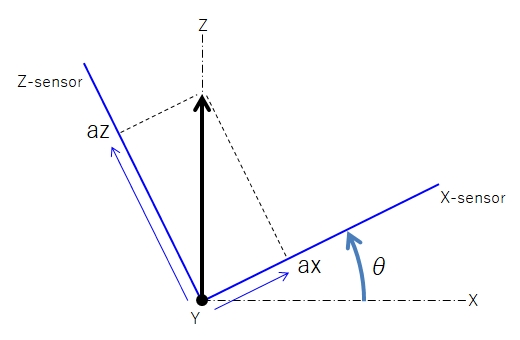
次は回転行列からオイラー角への変換です。
▼座標変換行列▼
\begin{align} \\ \begin{bmatrix} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \\ a_{20} & a_{21} & a_{22} \end{bmatrix} &= \begin{bmatrix} \cos\theta_y\cos\theta_z &\cos\theta_y\sin\theta_z &-\sin\theta_y \\ \sin\theta_x\sin\theta_y\cos\theta_z – \cos\theta_x\sin\theta_z &\sin\theta_x\sin\theta_y\sin\theta_z + \cos\theta_x\cos\theta_z &\sin\theta_x\cos\theta_y\\ \cos\theta_x\sin\theta_y\cos\theta_z + \sin\theta_x\sin\theta_z &\cos\theta_x\sin\theta_y\sin\theta_z – \sin\theta_x\cos\theta_z &\cos\theta_x\cos\theta_y \end{bmatrix} \\\\ \end{align}▲行列の各要素をこのように置いたとき、
\(\theta_x\)については、
\begin{align} \\ \frac{a_{12}}{a_{22}} &= \frac{\sin\theta_x\cos\theta_y} {\cos\theta_x\cos\theta_y}=\frac{\sin\theta_x}{\cos\theta_x}=\tan\theta_x\\\\\\ \theta_x &= \tan^{-1}\frac{a_{12}}{a_{22}} \\\\ \end{align}このようになります。
\(\theta_y\)については、
\begin{align} {a_{12}}^2+{a_{22}}^2 & = \sin^2\theta_x\cos^2\theta_y + \cos^2\theta_x\cos^2\theta_y\\\\ &=\cos^2\theta_y\left(\sin^2\theta_x + \cos^2\theta_x\right)\\\\ &=\cos^2\theta_y\\\\ \sqrt{{a_{12}}^2+{a_{22}}^2} &= \cos\theta_y\\\\ \frac{a_{02}}{\sqrt{{a_{12}}^2+{a_{22}}^2}} &= -\frac{\sin\theta_y}{\cos\theta_y}\\\\ &= -\tan\theta_y\\\\ \theta_y &= -\tan^{-1}\left(\frac{a_{02}}{\sqrt{{a_{12}}^2+{a_{22}}^2}}\right) \\\\ \end{align}となります。簡単に\(a_{02}\)からでも出せますが、6軸センサーなどから算出するのであれば複数値から算出した方が安定しそうなのでこうしてます。
最後に\(\theta_z\)については
\begin{align} \\ \frac{a_{01}}{a_{00}} &= \frac{\sin\theta_y\cos\theta_z} {\cos\theta_y\cos\theta_z}=\frac{\sin\theta_z}{\cos\theta_z}=\tan\theta_z\\\\\\ \theta_z &= \tan^{-1}\frac{a_{01}}{a_{00}} \\\\ \end{align}このようになります。
慣性センサーを使用して姿勢角度を算出するときに使いそうな行列式をまとめておきました。
▼参考サイト▼



コメント