EXCELでローパスフィルター（一次遅れ、ノイズ除去）

　EXCELで一次遅れのローパスフィルタ（ノイズ除去、平滑化）を行う方法です。マクロやVBは使わずにEXCELの表計算機能のみで行ってみたいと思います。

概要

　まずローパスフィルタの伝達関数を後退差分方式を用いて離散化（プログラム化）、整理すると

$$\begin{align} y_{\lbrack{n}\rbrack} = \frac{T_i}{T+T_i}y_{\lbrack{n-1}\rbrack}+\frac{T}{T+T_i}x_{\lbrack{n}\rbrack} \end{align}$$

となるようです。ここで、以下のように置いて

$$\begin{align} \frac{T}{T+T_i}=k \end{align}$$

　もとの式を変形していくと

$$\begin{align} y_{\lbrack{n}\rbrack} &= \left(1-k\right)y_{\lbrack{n-1}\rbrack}+kx_{\lbrack{n}\rbrack}\\\\ &=y_{\lbrack{n-1}\rbrack}+k\left(x_{\lbrack{n}\rbrack}-y_{\lbrack{n-1}\rbrack}\right) \end{align}$$

　このような形に整理できます。yが出力値でxが入力値。前回の出力値と今回の入力値を合成するような形です。この式を基にEXCELでフィルターを掛けていきます。

　さっそくEXCELで準備していきます。

定数を準備

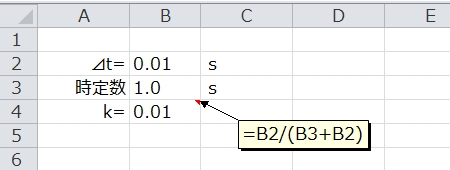
　例として、サンプリング周期は0.01s、時定数は1.0sにしてます。B4セルに「k」を 計算しておきます。

時間

　続いて時間を計算します。

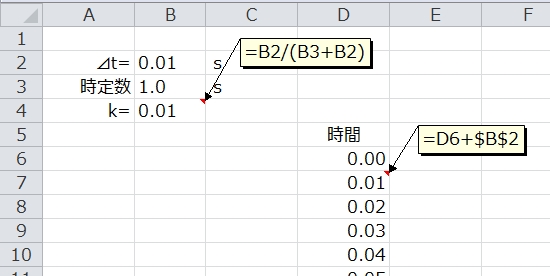
　D列に時間を計算しておきます。サンプリング周期 0.01s 刻みで10秒程まで作成しておきます。

入力

　入力を準備。

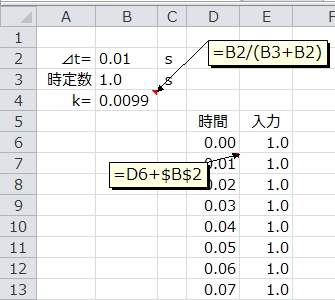
　E列に入力データを準備します。今回はずっと「1.0」の入力が続く想定をしてます。

出力（ローパスフィルタ）

　フィルタ通過後の出力値を計算します。

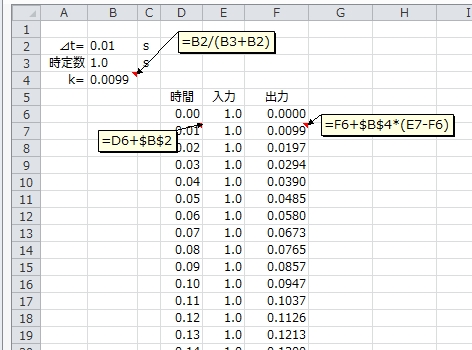
　F列に出力値を計算します。時刻0sの時は「0」を入力。その下7行目から、先ほどの離散化式に基づいて出力値を計算すればフィルタ後の出力完成。

グラフで出力確認

　先ほどの結果をグラフ化して確認してみます。

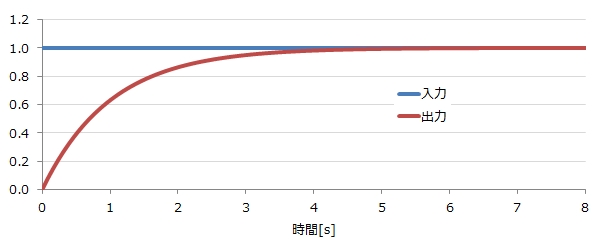
　時定数「1.0s」で、立ち上がりおおよそ0.63（63%）になっているので一応理論通りです。

　入力値に適当なノイズを入れてみました

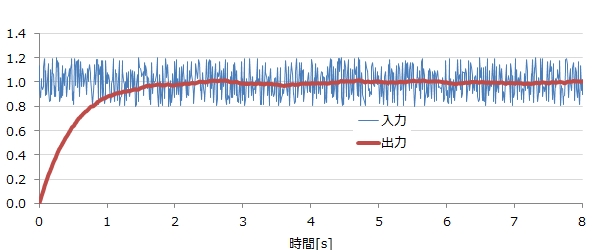
　サンプリング周期「0.01s」、時定数は「0.5s」にしてます。

　簡単にシミュレーション行うにはEXCELは手軽で便利です。がリアルタイム処理が不要なら、ローパスフィルターでなくてもいいかもしれません。