
ジャイロのドリフト補正を改良してみました。6軸センサー(ジャイロ、加速度センサー)から姿勢角を算出する際、ジャイロドリフトを加速度センサーから算出した姿勢角で補正してなるべく正確な姿勢角を算出すると思います。
ただセンサー自体に加減速がある場合、加速度センサーからの姿勢角算出がおかしくなってしまいます。
▼確認動画▼
センサー値をProcessingを使用して可視化してます。左が加速度センサーのみから算出した角度、右がジャイロから算出したものです。
センサー自体を揺らすと加速度センサーの方はおかしな角度となってしまいます。センサーの加速度を拾ってしまうためです。(加速度センサーから角度算出)
ジャイロの方は3軸ベクトルを合わせていない(z軸回転)のとドリフトが発生しているため最後にはかなりおかしな角度となってます。(6軸センサーから角度算出)
今回はこの加速度の影響をなるべく軽減できないかを相補フィルターを改良して試してみました。
まず普通?の相補フィルターですが
補正後角度 = 0.9 * (ジャイロセンサーからの角度) + 0.1* (加速度センサーからの角度)
係数は適当です。それぞれの算出角度に重み付け平均しているイメージです。
ここでセンサー自体に加減速が働いた場合、係数によっては、加速度センサーに影響が出てしまい、補正角度にも影響が出てしまいます。
そこで重み付けしている係数をセンサーの加速度に合わせて可変できるように式を少しいじります。
補正後角度 = (1-k) * (ジャイロセンサーからの角度) + k * (加速度センサーからの角度)
このような感じにして、 kの式を
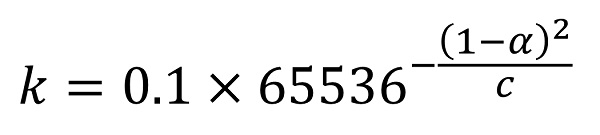
こんな感じにします。αはセンサーにかかる加速度、cは適当な係数です。その他の定数も適当です。(正規分布の公式をいじってます)
▼グラフ化すると▼
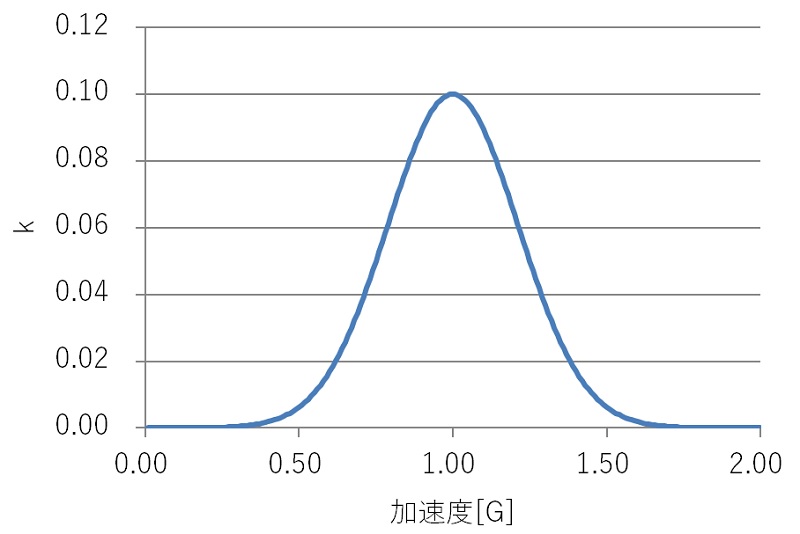
このような感じです。センサーの加速が1Gに近いときにドリフト補正を効かせて、加速が掛かっているときには重みを減らしている感じです。式の定数いじれば山なりの具合は変更できます。
こんな感じで補正したものの効果を確認してみました。
▼確認動画▼
左が改良したフィルター、右がカルマンフィルターです。
【捕捉】
カルマンフィルターはネット上に転がっていたライブラリを使用。中身がいまいちわからないため、係数はすべてデフォルトのままです。ですので、係数いじれば恐らくもっと加速の影響を消せると思います。
また普通?の相補フィルターでも重み付けの係数いじれば、この動画くらいの加減速であれば十分加速の影響を取り除けることは確認してます。ですので正確には本記事で紹介した方法がほんとに加速の影響を消せているかの確認はできていません・・・。

コメント
相補フィルタやカルマンフィルタは内容が難しい上、サイトも少ないので苦心していたところこちらのサイトを見つけることが出来たのでとても感謝しております…。
URL載せていただきありがとうございます!
そちらのサイトの論文も読んで参考にさせていただきます。
質問ばかりで申し訳ないのですが、簡易式のgxは角速度計測時の生データでしょうか?
生データの角速度積分値は物理的意味を持たないと指摘され、gxをdθ(オイラー角やロールピッチヨー角の微分値)に変換するような式を求めなければいけないのかと悩んでいるところなのです。。。
記事中の動画に関してはgx、gyは単純積分値を使ってます。おっしゃる通り姿勢角を検出する装置、またはその数値の利用方法によっては、各軸の生データの単純積算では全く意味をなさない場合があります。(動画内ではyaw軸に廻さないようにしてます)
3軸回転があるのであれば軸自体が回転してしまうため、オイラー角や四元数による角度算出は必要かと思います。コメント欄での説明は厳しいのでよろしければ次回にでも簡単な説明の投稿をしたいとおもいます。
やはり三軸回転の場合はオイラー角やクォータニオンを計算しないといけないんですね…。
次回のご投稿お待ちしております!
丁寧にご教示くださりありがとうございました!
研究で現在非常に困っているところでとても参考になっております!
丁寧な記事ありがとうございます。
3軸回転を考慮したときの説明を是非ともお願いしたいです。
宜しくお願い致します。
tmさん、コメント有難う御座います。
また記事を閲覧にきて頂いたのに削除しており申し訳ありません。
その後いろいろ検証を続けておりまして・・、ケースバイケースかと思いますが本記事の内容が悪影響する場合もあり、また相補フィルターも結構優秀で、、、、本記事内容程のことをしなくてもいい場合もあり・・。
誤解を生むといけないため削除しました。私の理解が不十分であり、ご迷惑をおかけ致します。
今のところ再公開の予定はありません。もし知りたい内容があるようであれば「問い合わせ」フォームからご連絡頂ければ可能な限り回答したいと思います。
返信ありがとうございます。
独自に両センサの重み付けの処理を行っていて、センサに加速が働く中でもかなり正確に角度の検出ができていたように記憶しております。
削除に関してはお考えあってのことでしょうから、どうかお気になさらず。強いて気になることと言えば、あのような重み付けを行う発想にどのようにして至ったのかが少し気になるくらいでしょうか。
今後の投稿も楽しみにしております。
重み付けの可変についてですが、カルマンフィルターが発想の元と言えばいいのか・・。カルマンフィルターも予測値を更新する際のゲインは可変させてると思います。今回、加速度センサー(角度)の精度が悪い状態は加速度値からわかります(加減速があるとき)。その具合に応じて係数を可変させてるという発想です。