3D回転を表現するAndroidアプリをMIT APP Inventor2で作成してみました。座標計算は回転行列ではなく四元数 (quaternion(クォターニオン))で計算してます。
▼アプリ動画▼
単純に6面体の3D回転を表示しているだけのソフトです。今回は2軸だけで試行してます。
最初はオイラー角、回転行列から座標計算して6面体を3D表示させようとしていたのですが、計算が面倒でMIT APP Inventor2のブロック図でプログラミングするのが大変で断念しました。
回転行列で6面体の回転を計算すると、座標点成分(8)、回転行列(3×3)、ローカル座標軸(3)、2軸回転(2)と単純に考えても非常に多くの計算が必要になります。そこで今回は回転計算が簡素になる四元数を使って座標計算を行いました。
四元数(quaternion(クォターニオン))
四元数の詳細な解説については、いろいろなサイトで解説されちますのでここでは結果だけ説明します。
四元数は
![]()
で実部(スカラー)と虚部(ベクトル部)で表現されます。
ベクトルx(x,y,z)を四元数で表現すると
![]()
となります。
任意の単位ベクトル(ax,ay,az)軸廻りにθ回転する四元数は
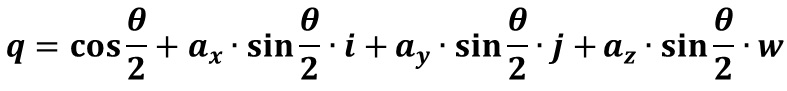
で表すことができ、共役四元数は虚部をマイナスにして
![]()
となります。
回転計算ですが回転させたいベクトルを、回転を表す四元数と共役四元数で挟み込むようにすれば計算できます。
ベクトルxを、回転を表す四元数qで回転させるには
![]()
と、このようになり、回転後のベクトルvが計算できます。回転行列に比べるとずいぶん計算が簡素になります。
また複数軸の回転について、回転qと回転pを行うには
![]()
このように回転を表す四元数を積しておけば、一度の回転計算で可能です。
ちなみに四元数の積は
![]()
![]()
実部をs、虚部をvと分けてこのような式で纏められます。「・」内積、「×」外積です。
内積、外積は

これで計算できます。
四元数を使用すれば回転行列より計算が簡素になり、またジンバルロックも起きないため3D回転等を表現するときは便利かと思います。

コメント