群衆アルゴリズム（Boid）をProcessingでやってみる

　いまさら感がありますが、フロッキングアルゴリズム（Boids）のプログラム（Processing）を試してみました。使い古された感はありますが、個人的に興味があったのと、（プログラムの）勉強を兼ねて行ってます。

概要

　フロッキングアルゴリズムとは（例えば魚や鳥など、）集団運動をシミュレートするアルゴリズムで今回はBoids理論と呼ばれるものを試してみました。

▼デモ動画▼

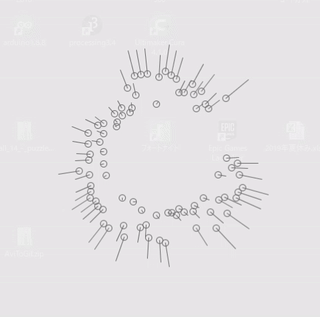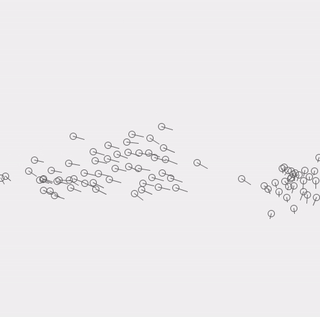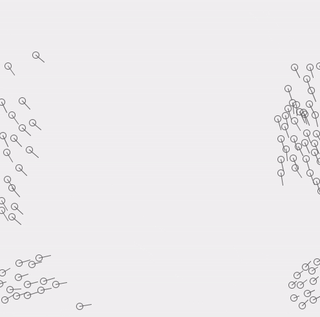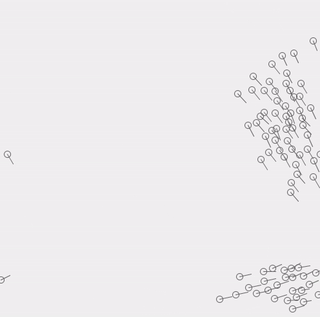
　実際に今回作成した物です。簡単な考え方で集団運動が再現できていろいろな分野で使われているアルゴリズムのようです。

　考え方ですが、以下3つのルールを適用するだけでシミュレートできるとのこと。実際に上の動画も以下のルールのみでシミュレートしてます。

各々の個体に対して、
１、群れの中心に向かう
２、周りと同じ方向、同じ速度になるように動く
３、互いに近づきすぎたら離れる

　といった３つのルールでできる方向ベクトルを重み付け合成し、各個体の動く方向と速度を決める、といったアルゴリズムです。実際には他にいろいろルールを追加して行うこともできるようですが、今回はこの基本の3つのルールでシミュレートしてます。

ソース解説

　プログラムはProcessingを使用。ルール部分のソースを抜粋して解説します。（ソース全体は記事最後に掲載してます。）

①群れの中心に向かう部分

▼ソース抜粋▼

  aveX = 0;
  aveY = 0;
  for (int i=0; i<num; i++) {
    aveX += x[i];
    aveY += y[i];
  }
  aveX /= num;
  aveY /= num;
  if (mousePressed == true) {
    aveX = mouseX;
    aveY = mouseY;
    stroke(0, 0, 255);
    fill(0, 0, 255);
    ellipse(aveX, aveY, 10, 10);
  } 

  for (int i=0; i<num; i++) {
    ctrDirX[i] = aveX - x[i];
    ctrDirY[i] = aveY - y[i];
  }

　単純に群れ（全個体）の平均の位置を中央位置と見立てて算出してます。この時の平均位置には自分の位置も含めてます。マウスクリックした場合は、その場所を中央にする、というような処理も加えてます。

　で最後に中央位置を各々自分からの方向と大きさ（ベクトル）に変えてます。

　よりリアルな動きにするため、近くの個体とか、視野にいる個体とかなどのルールも加えて中央位置を算出することもあるようです。

②周りと同じ方向、同じ速度になるように動く部分

▼ソース抜粋▼

  aveVel   = 0;
  aveAngle = 0;
  for (int i=0; i<num; i++) {
    aveVel   += sqrt(dx[i]*dx[i]+dy[i]*dy[i]);
    aveAngle += degrees(atan2(dy[i], dx[i]));
  }
  aveVel   /= num;
  aveAngle /= num;

  velX = aveVel*cos(radians(aveAngle));
  velY = aveVel*sin(radians(aveAngle));

　平均速度は「個々の前回の移動ベクトル」からスカラー量にして平均を算出してます。平均方向も「個々の前回の移動ベクトル」からいったん角度にして角度平均を算出してます。

　で最後に平均速度（大きさ）、平均方向（角度）をベクトルにしてます。

③互いに近づきすぎたら離れる

▼ソース抜粋▼

  for (int i=0; i<num; i++) {
    contX[i]=0;
    contY[i]=0;
    for (int j=0; j<num; j++) {
      if (i!=j) {
        float dist=sqrt((x[j]-x[i])*(x[j]-x[i])+(y[j]-y[i])*(y[j]-y[i]));
        if (0<dist&&dist<15) {
          contX[i] = -1*(x[j]-x[i]);
          contY[i] = -1*(y[j]-y[i]);
          float temp = sqrt(contX[i]*contX[i]+contY[i]*contY[i]);
          contX[i]/=temp;
          contY[i]/=temp;
        }
      }
    }
  }

　自分とそれ以外との距離を総当たりで確認して、距離が近かったら離れる方向のベクトルを確認してその方向ベクトルを正規化してます。

　このソースだと、距離15以下はすべてヒットしてしまい、複数の個体が近くにいた場合でも、最後に確認した個体と離れる処理になってしまいます。

　できれば一番近い個体から離れるようにして、しかも距離（近さ）に応じて反発する強さも制御したほうがいいかなとも思いましたが、ちょっと面倒くさくなってきたのでこのままいきました。

各個体の動く方向と速度を決める

　今まで算出してきたベクトルの重み付き合成和をとって個々の動く方向と速度決めます。

　▼ソース抜粋▼

  for (int i=0; i<num; i++) {
    kX[i] = 0.03*ctrDirX[i]+4.0*velX+5.0*contX[i];
    kY[i] = 0.03*ctrDirY[i]+4.0*velY+5.0*contY[i];

    float tempVel = sqrt(kX[i]*kX[i]+kY[i]*kY[i]);
    if (tempVel>2) {
      kX[i]=2*kX[i]/tempVel;
      kY[i]=2*kY[i]/tempVel;
    }

    dx[i] += (kX[i]-dx[i])*0.02;
    dy[i] += (kY[i]-dy[i])*0.02;

    x[i] += dx[i];
    y[i] += dy[i];
  }

　最初にそれぞれのベクトル（①中心に向かう、②周りと速度、方向合わせる③近づいたら離れる）の合成和をとってます。重み付けの係数は適当です。この係数の大きさで各個体の動き方が大きく変わります。

　次に速度が出すぎないように制限かけてます。ここでは「2」以上の速度が出ないようにしてます。

　で移動量（ベクトル）はフィルターをかけるイメージでゆっくり滑らかな変化になるように処理を加えて、各々の位置へ反映してます。

　あとはこの処理の繰り返しです。この内容で記事冒頭にあるような動画処理を行ってます。割と簡単なアルゴリズムで群れの動きが再現できてすごいです・・。

ソース全体

　今回の動画に使ったProcessingのプログラム全体です。独学なので解釈が間違ってるかもしれませんが・・・・・。

▼ソース全体▼

int num = 80;

float[] x  =new float[num];
float[] y  =new float[num];
float[] r  =new float[num];
float[] dx  =new float[num];
float[] dy  =new float[num];

float[] ctrDirX =new float[num];    
float[] ctrDirY =new float[num];    
float[] vel =new float[num];
float[] velAngle =new float[num];
float[] contX =new float[num];    
float[] contY =new float[num];    
float[] kX =new float[num];    
float[] kY =new float[num];    

float aveX, aveY, aveAngle, aveVel;
float velX, velY;

void setup() {
  for (int i=0; i<num; i++) {
    r[i]     = 10;
    x[i]     = 250+80*cos(radians((360/num)*i));
    y[i]     = 250+80*sin(radians((360/num)*i));
    velAngle[i] = (360/num)*i;
    vel[i]   = random(0, 5.5);
    dx[i]    = vel[i]*cos(radians(velAngle[i]));
    dy[i]    = vel[i]*sin(radians(velAngle[i]));
  }

  size(500, 500);
  background(240);
  smooth();
}

void draw() {
  background(240);
  stroke(100);
  strokeWeight(1);
  noFill();
  for (int i=0; i<num; i++) {
    ellipse(x[i], y[i], 10, 10);
    line(x[i], y[i], x[i]+10*dx[i], y[i]+10*dy[i]);
  }

  aveX = 0;
  aveY = 0;
  for (int i=0; i<num; i++) {
    aveX += x[i];
    aveY += y[i];
  }
  aveX /= num;
  aveY /= num;
  if (mousePressed == true) {
    aveX = mouseX;
    aveY = mouseY;
    stroke(0, 0, 255);
    fill(0, 0, 255);
    ellipse(aveX, aveY, 10, 10);
  } 

  for (int i=0; i<num; i++) {
    ctrDirX[i] = aveX - x[i];
    ctrDirY[i] = aveY - y[i];
    //stroke(0, 0, 255);
    //line(x[i], y[i], x[i]+0.1*ctrDirX[i], y[i]+0.1*ctrDirY[i]);
  }
  //stroke(0, 0, 255);
  //fill(0, 0, 255);
  //ellipse(aveX, aveY, 10, 10);

  aveVel   = 0;
  aveAngle = 0;
  for (int i=0; i<num; i++) {
    aveVel   += sqrt(dx[i]*dx[i]+dy[i]*dy[i]);
    aveAngle += degrees(atan2(dy[i], dx[i]));
  }
  aveVel   /= num;
  aveAngle /= num;

  velX = aveVel*cos(radians(aveAngle));
  velY = aveVel*sin(radians(aveAngle));

  //stroke(0, 255,0);
  //for (int i=0; i<num; i++) {
  //line(x[i], y[i], x[i]+60*velX, y[i]+60*velY);
  //}

  for (int i=0; i<num; i++) {
    contX[i]=0;
    contY[i]=0;
    for (int j=0; j<num; j++) {
      if (i!=j) {
        float dist=sqrt((x[j]-x[i])*(x[j]-x[i])+(y[j]-y[i])*(y[j]-y[i]));
        if (0<dist&&dist<15) {
          contX[i] = -1*(x[j]-x[i]);
          contY[i] = -1*(y[j]-y[i]);
          float temp = sqrt(contX[i]*contX[i]+contY[i]*contY[i]);
          contX[i]/=temp;
          contY[i]/=temp;
        }
      }
    }
  }
  //for (int i=0; i<num; i++) {
  //stroke(255, 0, 0);
  //line(x[i], y[i], x[i]+contX[i], y[i]+contY[i]);
  //}

  for (int i=0; i<num; i++) {
    kX[i] = 0.03*ctrDirX[i]+4.0*velX+5.0*contX[i];
    kY[i] = 0.03*ctrDirY[i]+4.0*velY+5.0*contY[i];

    float tempVel = sqrt(kX[i]*kX[i]+kY[i]*kY[i]);
    if (tempVel>2) {
      kX[i]=2*kX[i]/tempVel;
      kY[i]=2*kY[i]/tempVel;
    }

    dx[i] += (kX[i]-dx[i])*0.02;
    dy[i] += (kY[i]-dy[i])*0.02;

    x[i] += dx[i];
    y[i] += dy[i];

    if (x[i]>500)x[i]=0;
    if (x[i]<0)x[i]=500;
    if (y[i]>500)y[i]=0;
    if (y[i]<0)y[i]=500;
  }
}