
Arduinoのライブラリにカルマンフィルターがあるのですが、中身がどういうことをやっているのか勉強を兼ねて見てみました。
IDEでライブラリ検索するとカルマンフィルターでいくつかヒットするのですが、今回はこのライブラリのプログラム(ソース)をカルマンフィルターの説明を加えながら見てみたいと思います。
https://github.com/TKJElectronics/KalmanFilter
このカルマンフィルターですが、加速度、角速度と制御周期を入力として、カルマンフィルターを通して、きれいな角度を推定しているライブラリとなります。ただ後述しますが、このライブラリは3軸(3D)回転がある場合には対応していないようですね。
カルマンフィルターの説明を加えながら中身を見ていきたいと思います。(説明といっても基本式を展開して、ソースと一致しているか見ているだけです・・・。)
状態空間モデル
▼状態方程式はこんな感じで定義しているようです▼
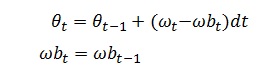
(※以降、添え字は適当です。無視して下さい・・・。)
ωbはバイアス誤差です。
▼それぞれこのように置いて▼
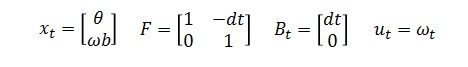
▼行列で表現すると▼
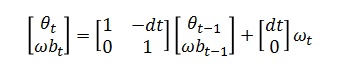
このような感じになります。状態ベクトルは角度とバイアス誤差、入力は角速度で定義。バイアス誤差は直接測定できないので、過去の値を持ってくるようです。少し腹落ちしない感じですが、、、。
▼観測方程式は▼
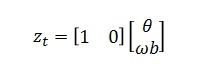
加速度センサーから角度を観測してます。
ここからライブラリのソースと絡めて見ていきたいと思います。(式を展開していき、ソースと一致していくか見ていきます)
ステップ毎に見ていきたいと思います。まずは予測ステップから。
STEP1(状態の予測)
▼ソース▼
/* Step 1 */ rate = newRate - bias; angle += dt * rate;
角速度から角度計算している部分です。ソースの表現(式)を少し変えてみると
angle = angle + dt*(newRate -bias);
となって、状態方程式
![]()
と同様です。単純に角速度(バイアス誤差を加味)からの積算で現在の角度を予測してます。
STEP2(誤差共分散の予測)
▼ソース▼
/* Step 2 */ P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle); P[0][1] -= dt * P[1][1]; P[1][0] -= dt * P[1][1]; P[1][1] += Q_bias * dt;
誤差共分散の予測部のソースはこのようになってます。
カルマンフィルターの式に当てはめていくと

となって、ソースと同様になります。
ここから更新ステップを見ていきます。
STEP3(観測残差)
▼ソース▼
/* Step 3 */ float y = newAngle - angle; // Angle difference
このようになってます。「観測値(加速度からの角度)」から「STEP1で予測した角度」の差分となります。
観測残差の当てはめて、式を展開していくと
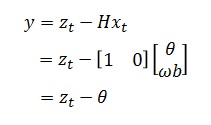
このようになります。少し腹落ちしないですが、ソースと同様なので間違いではないのかと・・・。
STEP4(観測残差の共分散)
▼ソース▼
/* Step 4 */ float S = P[0][0] + R_measure; // Estimate error
ソースはシンプルですね。
カルマンフィルターの式に当てはめて展開していくと

このようになってソースと一致します。
STEP5(カルマンゲインの更新)
▼ソース▼
float K[2]; // Kalman gain - This is a 2x1 vector K[0] = P[0][0] / S; K[1] = P[1][0] / S;
ここもソースはシンプルですね。
同様にカルマンフィルターの式を展開していくと
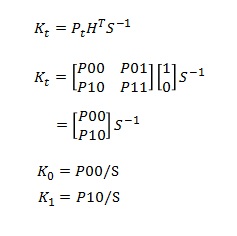
2×1の行列となり、ソースと同様です。
STEP6(状態の更新)
▼ソース▼
/* Step 6 */ angle += K[0] * y; bias += K[1] * y;
予測値を更新している部分です。角度、バイアス誤差の更新をしてます。
カルマンフィルターの式から展開していくと
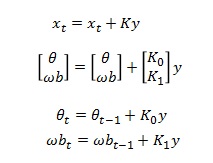
このような感じになり、ソースと同様になりますが、ここも少し消化不足です・・・。
STEP7(誤差共分散の更新)
▼ソースではこのように計算してます▼
/* Step 7 */ float P00_temp = P[0][0]; float P01_temp = P[0][1]; P[0][0] -= K[0] * P00_temp; P[0][1] -= K[0] * P01_temp; P[1][0] -= K[1] * P00_temp; P[1][1] -= K[1] * P01_temp;
最後に誤差共分散の更新です。
これも同様に公式に当てはめて展開していくと
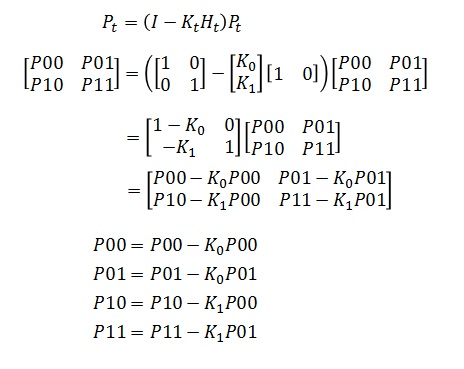
ソースと一致します。
説明は以上です。これを繰返し更新していくことで状態を推定・更新していきます。私の理解不足なのか、所々腹落ちしていないのですが、全体がシンプルなソースでわかり易くカルマンフィルターの流れを理解するには分かりやすいかもしれせん。
ただこのフィルター、角速度を単純に積算していて、座標系(センサー、絶対軸)のズレを考慮していません。なので3軸回転には追従しないと思います。加速度センサーではz軸(yaw)回転も算出できないため、z軸回転の補正には別途、地磁気センサー等で角度入力をしないといけないようです。
使用するときにはこの辺に注意した方がよさそうです。
参考サイト

コメント