プログラムでフィルタ（平滑化、ノイズ除去）の遅れを無くす

　プログラムで簡単な平滑フィルタ（ローパスフィルタ）を通して、計測値の平滑化、スムージング、ノイズ除去などをよく行うのですが、マイコンなどで計測値をリアルタイム処理する場合にはどうしても遅れなどが、発生してしまいます。

　今回はあまり遅れが出ないように、フィルタを少し改造して試してみました。

ローパスフィルタ（プログラム）で遅れの確認

　サンプル（計測値）にまずは普通？のローパスフィルタを通してEXCELでシミュレーション（グラフ化）してみます。

  LPF = (1 - k) * lastLPF + k * raw;
  lastLPF = LPF;

  //lastLPF：前回のLPF値
  //raw ：今回の計測値

　フィルタを言語風に書くとこんな感じでしょうか。「前回の補正値」と「今回の計測値」を重み付け平均している感じです。「ｋ」は定数。（0 ≦ k ≦ 1）

▼式を展開して纏め直すと▼

  LPF += k * (raw - lastLPF);

　このような速度から積分してるっぽい式？になります。ですので「ｋ」（時間）の値を小さくすればするほど遅くなる・・（イメージです・・。）

　ではこの式とEXCELを使ってフィルターの簡単なシミュレーションをしてみます。

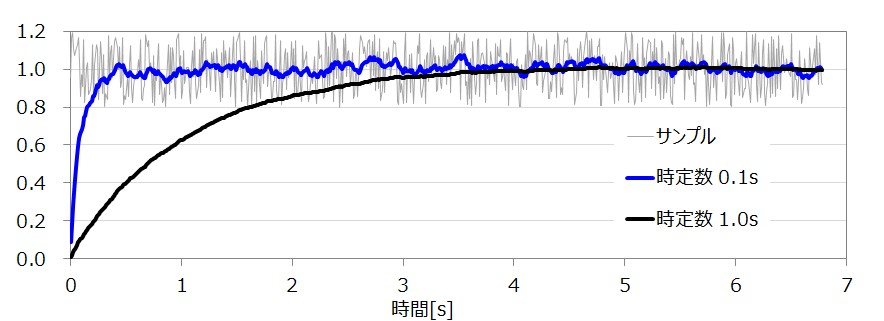
▲シミュレーション結果。入力値を 1（＋適当なノイズ）、サンプリング周期 0.01s（100Hz）、でシミュレーションしてます。収束を早くすると平滑化しきれてません（時定数0.1s）が、きれいに平滑化しようとすると立ち上がりが遅れます（時定数1.0s）。

　ここから一手間加えて、この遅れを少しでも軽減してみたいと思います。

　少し横道にそれますが先ほどのプログラムの元式を簡単に解説です。結果のみで良い方はこの項は飛ばして下さい。

　まず、ローパスフィルタの伝達関数を後退差分方式を用いて離散化（プログラム化）、整理すると

\begin{align} y_{\lbrack{n}\rbrack} = \frac{T_i}{T+T_i}y_{\lbrack{n-1}\rbrack}+\frac{T}{T+T_i}x_{\lbrack{n}\rbrack} \end{align}

▲このようになるようです。yはフィルタ後、ｘは計測値、Tはサンプリング周期、Tiは時定数。

▼ここで計測値xの係数をkとして

\begin{align} \frac{T}{T+T_i}=k \end{align}

▼yの係数を変形すると

\begin{align} \frac{T_i}{T+T_i}=1-\frac{T}{T+T_i}=1-k \end{align}

このようになり、元の式を

\begin{align} y_{\lbrack{n}\rbrack} = \left(1-k\right)y_{\lbrack{n-1}\rbrack}+kx_{\lbrack{n}\rbrack} \end{align}

と変形しているだけです。これが先ほどの言語式と同様です。

　ではフィルターを改造して、遅れを少しでも無くしてみたいと思います。方法としては、随時、「測定値」と「補正値」を比較し、差が大きいようであれば、定数「k」（速度）を変更するといった処理を加えてみます。

　▼言語風に記述すると▼

  if (abs(raw - LPF) > 0.33) {
    k = 0.0909;
  }
  else {
    k = 0.0099;
  }
  LPF += k * (raw - LPF);

　「今回の測定値」と「前回の補正値」の差分が大きいようであれば、定数「k」の値（時定数 0.1s/1.0s ）を変えます。差分の判定値は適当です。誤差の分散などをみて適宜調整が必要かと思います。

　この考え方で先ほどの同様のグラフ（計測値）に、フィルタを通してみます。

▼フィルタ（改）後グラフ▼

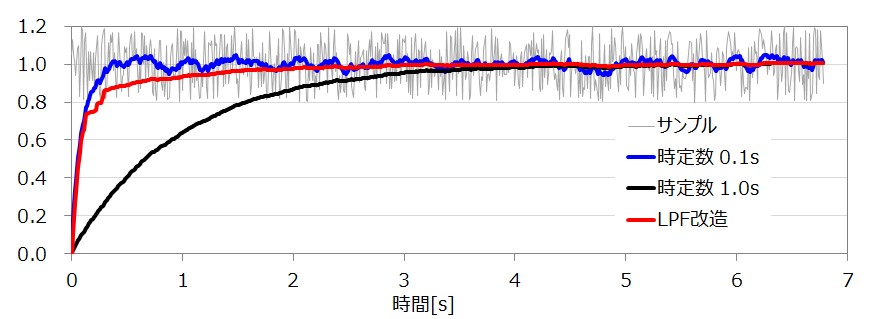
赤ラインが一手間加えたフィルタを通したものです。

　立ち上がりで少しガタツキが出てしまってますが、遅れはだいぶ解消しているのではないかと思います。なるべく平滑化したいけどあまり遅れるのは困るということきに使えるかも・・・。

　ここでは測定値と補正値の差分で単純に定数「kの値」を切り替えてるだけですが、定数「k」を「差分」の関数で置いたら、もう少し立ち上がりも滑らかになるかもしれません。

　また今回は、適当に作ったサンプルデータをEXCEL上で計算して試してみただけです。実際試したわけではないのでここまでうまくいくかどうかわかりませんが、そのうち機会（必要なとき）があったら試してみたいと思います。

▼参考サイト▼