Processingで外サイクロイドを描画するプログラム

　前回、EXCELで外サイクロイド（エピサイクロイド）を描いたのですが今回はProcessingで軌跡を描いてみました。なるべく簡素に記述したつもり。そのソースコードを簡単に紹介します。

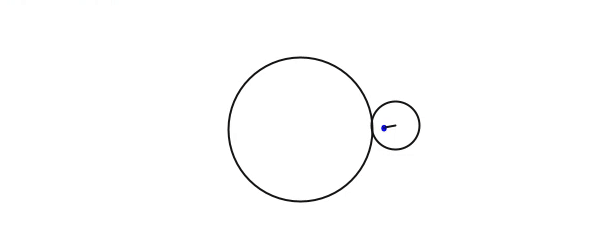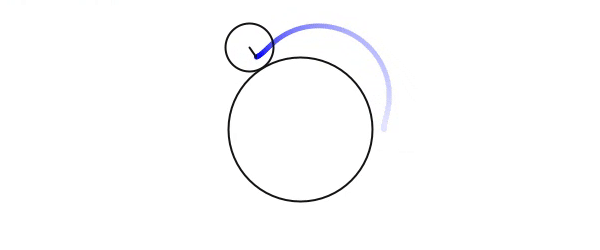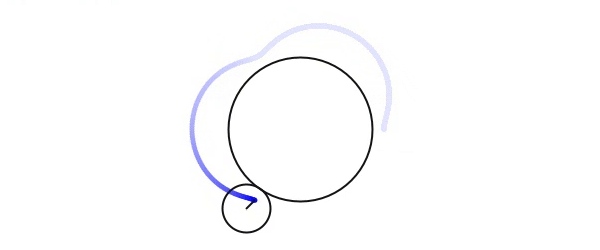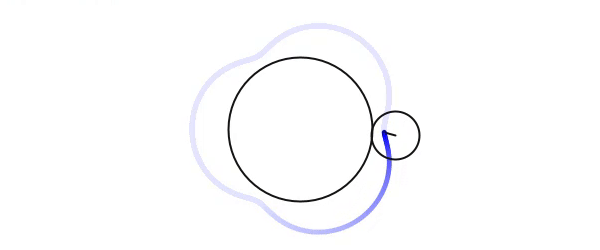
　Processingで作成した物のGIF画像です。径3:1の外サイクロイド。軌跡は前回算出した式をそのまま使用してます。

\begin{align} x&=\left(R+r\right)\cos{\theta}-r_q\cos{(\frac{R+r}{r}\theta)}\\\\ y&=\left(R+r\right)\sin{\theta}-r_q\sin{(\frac{R+r}{r}\theta)} \end{align}

ソースコード

　Processingのソース。先のGIF画像のものそのままです。ra：定円径、rb：動円径、rc：動円の軌跡点径です。incで回転速度が調整できます。rb=rcにすると動円周上の外サイクロイドになります。座標系の関係で角度はマイナスにインクリメントしてます。

//2025/12/12 imo Lab.
//https://garchiving.com

PGraphics pg1;
float ra, rb, rc;
float x, y, x1, y1, x2, y2, deg, inc;

void setup() {
  size(600, 250);
  pg1 = createGraphics(600, 250);
  ra=72;
  rb=24;
  rc=12;
  deg=0;
  inc=1;
  noFill();
  stroke(20);
  strokeWeight(2);
}

void draw() {
  x= (ra+rb)*cos(radians(deg));
  y= (ra+rb)*sin(radians(deg));
  x1= (ra+rb)*cos(radians(deg))-rb*cos(((ra+rb)/rb)*radians(deg));
  y1= (ra+rb)*sin(radians(deg))-rb*sin(((ra+rb)/rb)*radians(deg));
  x2= (ra+rb)*cos(radians(deg))-rc*cos(((ra+rb)/rb)*radians(deg));
  y2= (ra+rb)*sin(radians(deg))-rc*sin(((ra+rb)/rb)*radians(deg));

  background(255);

  pg1.beginDraw();
  if (deg==0) pg1.background(255);
  pg1.fill(255, 5);
  pg1.rect(0, 0, width, height);
  pg1.noStroke();
  pg1.fill(0, 0, 255);
  pg1.ellipse(x2+width/2, y2+height/2, 5, 5);
  pg1.endDraw();
  image(pg1, 0, 0);

  ellipse(width/2, height/2, ra*2, ra*2);
  ellipse(x+width/2, y+height/2, rb*2, rb*2);
  line(x+width/2, y+height/2, x2+width/2, y2+height/2);

  deg -=inc;
  if (deg<-360) deg = 0;
}