
Excelの表計算機能のみで微積分の計算をしてみました。微分積分と聞くと何やら難しいですがExcelで近似するだけなら割と簡単です。
基本的には微積分計算には公式があるのでそれを利用すればよいのですが、たまに計測値などから微積分したいことがありまして・・、数式化できないような値や簡単には微積分計算できない場合もあります。
この手の数値解析はいろいろ方法があると思いますが今回はExcelで行ってみたいと思います。
微分
微分のやり方からです。
例題としてまずは数式(微分計算)から答えをグラフ化してみます。
例えば、y=x^3-4x^2+3xを微分してみると、答えはy’=3x^2+8x+3となります。でそれぞれグラフ化してみます。
▼グラフ▼
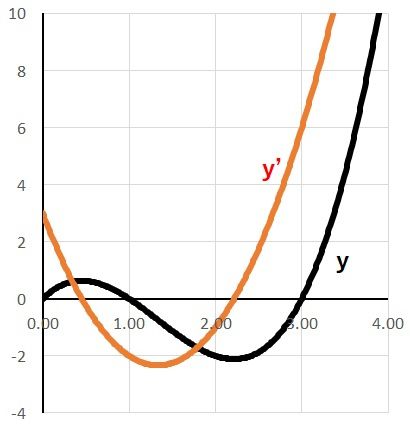
元と微分したものラインをならべてます。
でこの微分を理論計算からではなく、Excelの表計算から作成していきたいと思います。微分とは何か?と考えるとイメージつきやすいです。
▼微分は傾き▼
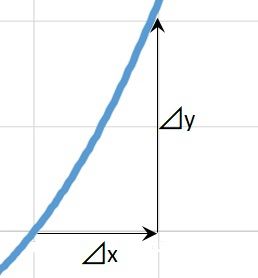
微分は傾きです。(ごく微小の変化率です)。ここでいう⊿y/⊿xが変化率になります。この⊿xを限りなく「0」に近づけたら微分(傾き)となります。
ですからExcelではなるべくx軸の値を小さくして、⊿y/⊿xを計算すれば微分(微分の近似値)が計算できます。では実際にExcelの表計算をしていきたいます。
まずはx軸の値を準備します。なるべく小さ目に0.01刻みで準備します。(計算機により精度の限界があるよう。)
▼x値▼
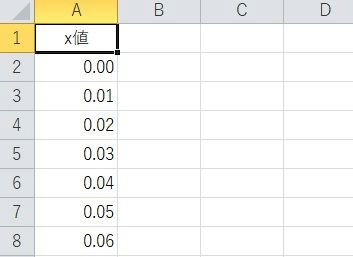
x軸の値をA列に準備します。単純に「A2セル」から順に「0」スタートで「0.01」刻みで増えていくだけです・・。仮に「0」からスタートしてますが、マイナス値からでも問題ありません。適当なところまで計算しておきます。(4くらい?)
次に微分する前の、元の式(y=x^3-4x^2+3x)を計算します。
▼y値▼
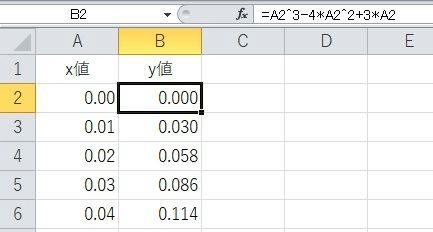
B列に微分前の数式「y=x^3-4x^2+3x」を計算します。「B2セル」に「=A2^3-4*A2^2+3*A2」と入れてドラックするだけです。(B1セル入力後(確定後)に選択枠右下の黒点(ドラックするときに掴む点)をダブルクリックすると一気に計算できます。何気に便利です。)
これで微分計算する準備が完了です。
▼微分(y’)▼
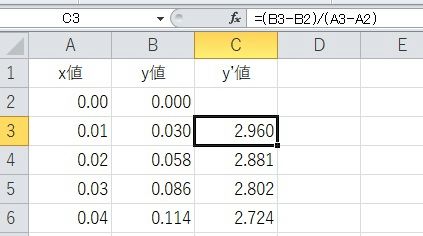
ではC列に微分計算していきます。最初のC2セルは(1個前の値が無いため)空欄にしておきます。「C3セル」から微分計算していきます。
先ほどの、⊿y/⊿xがそのまま微分計算となりますので「y変化分/x変化分」となります。ですから「C3セル」には「=(B3-B2)/(A3-A2)」と入力します。
ドラッグしたら微分(の近似計算が)完了です。簡単ですね。
▼一応先ほどの理論値計算したグラフと重ねると▼
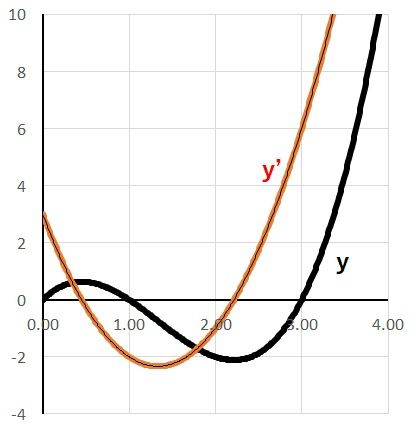
わかり難いですが目視ではほぼ一致してます。今回の例ではだいたい10分の1桁くらいまでは近似できます。もっと精度が欲しければx値の刻み方を細かくすればO.Kです。ただ、計算機により精度の限界があるようです。
微分は以上です。続いて積分の方法です。
積分
まずは先ほどの微分と同様に理論式で積分をグラフ化してみます。数式「y=x^3-4x^2+3x」を積分すると「∫y=1/4x^4-4/3x^3+2/3x^2」となります。でそれぞれグラフ化してみます。
▼積分グラフ化▼
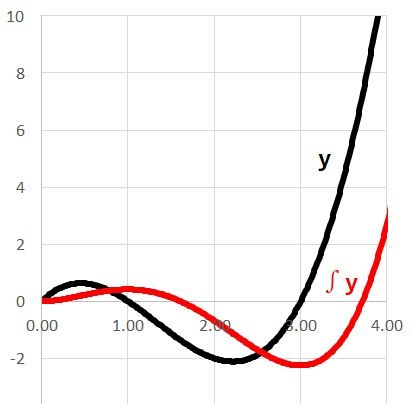
元のラインとそれを積分したものです。
でこの積分を理論計算からではなく、Excelの表計算から作成していきたいと思います。まずは考え方です。
▼積分は面積▼
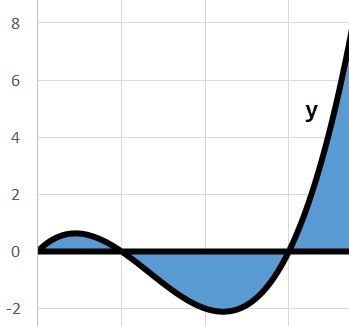
積分は面積です。ここでは曲線(y)とx軸で囲まれた部分の面積が積分値となります。この面積をExcelで表計算してきます。
▼面積の近似▼
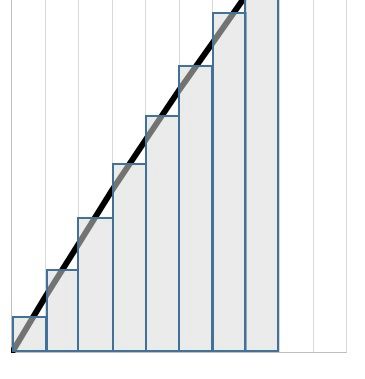
面積を計算する方法はいくつかありますがここでは簡単に(極細の)長方形の面積を足し算(積算)していく方法で行います。上図のような考えで面積を計算して積み上げていきます。
長方形の面積なので単純に縦×横で「Y×X」です。ここで「xの増分」を限りなく「0」に近づけると面積の精度が良くなるのがわかると思います。ただし微分同様、計算機による精度の限界はあるようです。ではExcelで表計算していきます。
元ラインは微分の時と同様のものを使用しますので、先ほど微分で作成したA列、B列はそのまま使用します。
▼面積(積分)計算▼
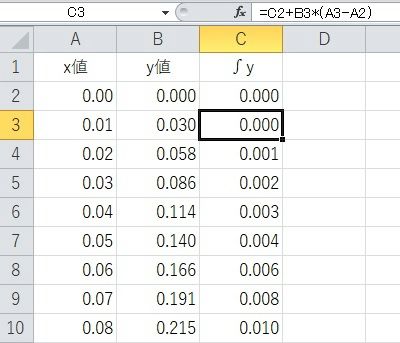
C列に面積(積分の近似値)を計算していきます。C2セルは「0」とします。C3セルに「=C2+B3*(A3-A2)」と入力。長方形の面積「横(x増分)×縦(y値)」を計算して、今までの面積に足していきます。下までドラックすれば積分の完了です。
▼一応先ほどの理論値計算したグラフと重ねると▼
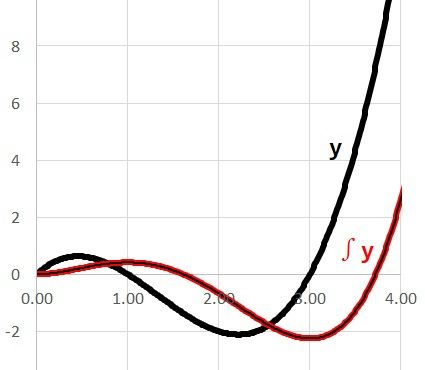
ほぼ一致してます。x軸のプロット間隔を小さくすればするほど精度は増していきます。今回は長方形の面積で行いましたが、他にも台形の面積計算でやる方法などがあります。(数値積分)
微分積分とも近似値となってしまいますが、測定値など式化できない数値から微積分を行いたい場合や、簡単には微積分計算できない場合など、Excelを使用すれば割と簡単に行えるかと思います。
説明に使ったEXCELシートはここからダウンロードできます。

コメント