
atan2(arctan2)の処理を高速化してみました。最近のCPUではどうかわかりませんが、Arduino等(ATmega328Pなどのマイコン)ではクロック周波数が非力なため、三角関数などの処理には時間がかかります。三角関数の中でもとくにatan2は処理時間がかかるため、高速化できないかを試してみました。
メモリもあまり無いですし、テーブル使わずに高速化を行ってみました。結果として精度は±0.01°以内、処理速度は2倍程早くなってます(ソースは記事途中で掲載してます。速度比較はArduinoIDEの標準ライブラリと比較)。まあ精度は落ちますが、それなりの高速化です。使い道によっては十分かと・・・・。(後述しますが、精度を犠牲にすればもう少し高速化できます)
atan2(arctan2、アークタンジェント2)とは
基本的にはatan(arctan、アークタンジェント、逆正接)と同様の意味合いにはなります。入力と出力が少し違うだけです。
atanは底辺、高さ(x座標、y座標)の「比」、から「角度」(ラジアン)をだすのに対して、atan2は「x座標、y座標の2値」から「角度」を出力します。
そのため、atanでは -π/2~π/2 までしか出力できませんが、atan2では座標値が入力となっているため-π~π(第1~4象限)まで出力できます。(x、yでそれぞれ符号が確認できるため)
標準ライブラリなどを使ったatan2関数のプログラム処理には結構時間が掛かります。今回はこの処理時間を近似式を使って高速化したいと思います。
近似式
まずは、y=arctan(x)*180/PIをグラフ化して、その近似式を見てみました。
▼逆正接のグラフ▼
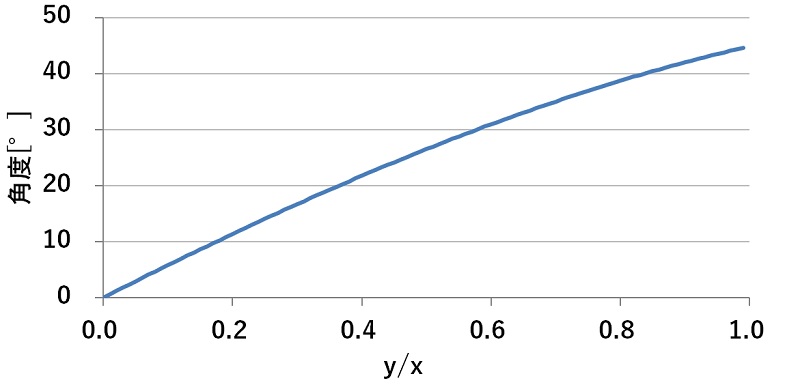
あえて0°~45°の範囲をグラフ化してます。でExcelで近似式を計算させると、
y = 8.2975*x*x*x*x - 20.114*x*x*x + 0.5812*x*x + 57.412*x
こんな感じです。今回は4次曲線で近似してます。
▼近似式を重ねたところ▼
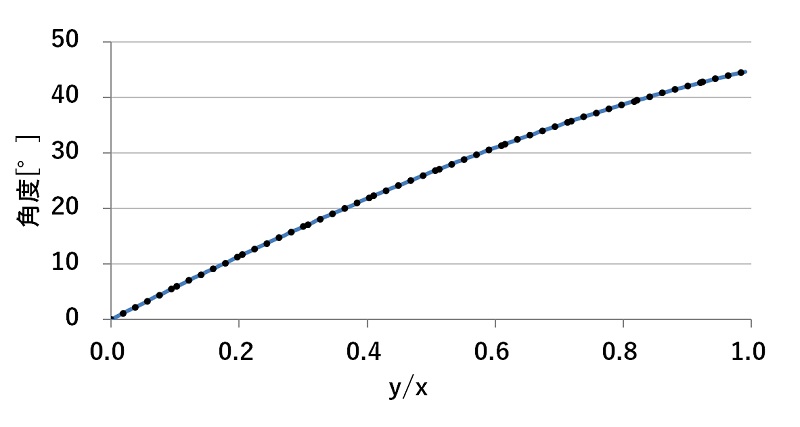
黒点が近似曲線です。ずれが目視ではわからないほどきれいに重なってます。(Excelで計算した近似式を少し手直ししてます)
誤差が目視ではわからないので、4次曲線(近似)とatanとの差分をグラフ化して重ねてみました。
▼誤差確認▼
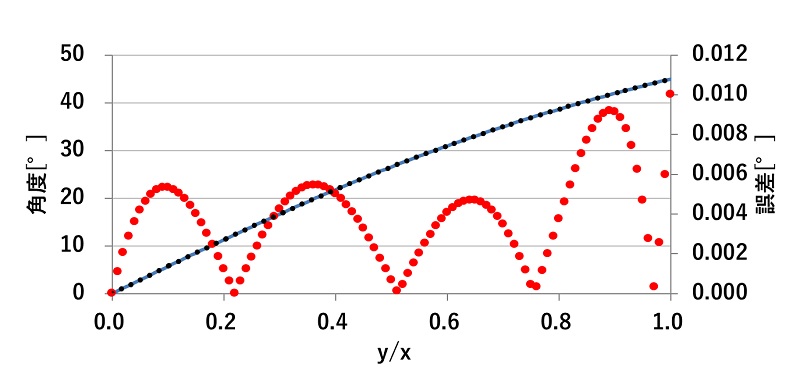
差分の絶対値をグラフ化してます。赤点が誤差です。±0.01°以内の近似値です。なるべく近似曲線を正確に出したかったので0°~45°の範囲としてます。それ以上長いとなかなか数次曲線では近似できなかったです。(誤差が大きくなる。)
45°~90°の範囲は反転したものと同様ですし、象限はx、yの符号確認して位相ずらせば良いのでそこらへんはプログラム側で持たせてます。
▼作成した関数▼
/// 2018/03 imo lab.
/// https://garchiving.com
int16_t _atan2(int16_t _y, int16_t _x) {
int16_t x = abs(_x);
int16_t y = abs(_y);
float z;
bool c;
c = y < x;
if (c)z = (float)y / x;
else z = (float)x / y;
int16_t a;
//a = z * (-1556 * z + 6072); //2次曲線近似
//a = z * (z * (-448 * z - 954) + 5894); //3次曲線近似
a = z * (z * (z * (829 * z - 2011) - 58) + 5741); //4次曲線近似
if (c) {
if (_x > 0) {
if (_y < 0)a *= -1;
}
if (_x < 0) {
if (_y > 0)a = 18000 - a;
if (_y < 0)a = a - 18000;
}
}
if (!c) {
if (_x > 0) {
if (_y > 0) a = 9000 - a;
if (_y < 0) a = a - 9000;
}
if (_x < 0) {
if (_y > 0) a = a + 9000;
if (_y < 0) a = -a - 9000;
}
}
return a;
}
戻り値の単位は、「度」ですが100倍した値(-18000~0~18000)を戻り値としてます。(意味はありません。あ、ゼロ除算の回避忘れてます。。。)
近似式は因数分解してます。効果無いかと思ったのですが、思いのほか速度効果がありました。
Arduino(IDE)で標準ライブラリと速度比較したところ、ライブラリ260μs×近似式120μsと、約半分(2倍程度)処理速度が向上しました。(ざっくりした測定方法です。)
ちなみに3次曲線で近似すると精度は±0.1°以内で処理速度は2.6倍程(100μs)。2次曲線で近似すると精度は±0.23°程で速度は3倍以上(80μs)と精度を犠牲にすればさらに速度は向上できます。
場合によっては十分な精度ですし、非力なCPUなどで少しでも高速処理したい場合に使えるかと思います。

コメント
はじめまして。
このサイトを参考にさせていただき、atan2関数と同じ働きをすることができる関数を作ることができました。ありがとうございます。
1つわからないことがあるのですが、この関数の時間を測定する際、どのような方法で行われたのでしょうか?
私はmicros()を使用して計測しようとしたのですが、それではうまく行きませんでした。
ざっくりでも、教えていただければ幸いです。よろしくお願いします。
白濱さん、サイト拝見下さり有難うございます。
私もmicros()を使用して測定する場合が多いですね。
ざっくりした計測になりますが、例えばこんな感じで、
Timer = micros();処理内容
dt = micros() - Timer;
測定したい内容を挟んで計測したりしてます。