
数値微分の精度をEXCELを使って比較してみます。
数値微分に前方差分、後方差分や中心差分という種類があることを最近知りました。今まで特に気にせず、というかそういった種類があることも知らずに後方差分というやり方で行ってきたようなのですが、中心差分の方が精度がいいとのこと。どれくらい精度が違うのかEXCELを使って比較してみました。
今回は \(\sin\) カーブを使って数値微分してみます。三角関数の公式より\(\sin\)の微分は、\(\left(\sin x\right)^{\prime}=\cos x\)なので、数値微分したものと\(\cos\)カーブを比較してみます。
▼まずは普通に\(\sin\)カーブと\(\cos\)カーブをEXCELで準備▼
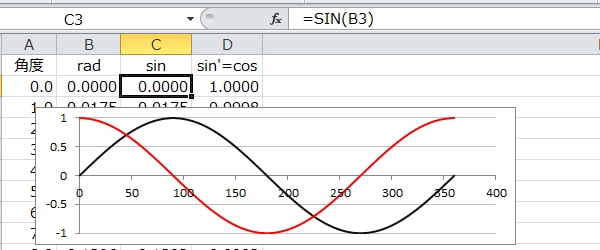
黒線が\(\cos\)カーブで\(\sin\)を微分した理論値となります。この\(\cos\)カーブと数値微分した値にどれほどの誤差があるかを確認してみたいと思います。
前方/後方差分
まずは前方/後方差分です。
\begin{align} f^{\prime}(x)\approx\frac{f(x)-f(x-h)}{h} \end{align}後方差分の式です。x点とその後方の点から微分値を近似します。前方差分とほとんど変わらないので個人的によく使う後方差分で精度をみます。今回\(h\)は1°(1rad)で刻みます。
▼精度確認(後方差分)▼
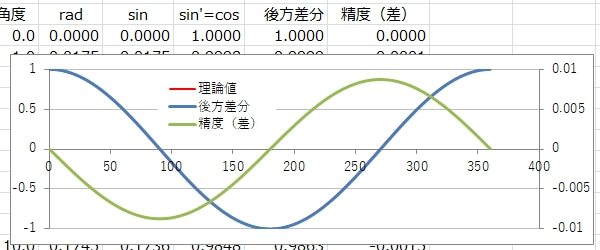
理論値と後方差分の近似値をグラフで重ねてみました。目視ではよくわからないので、差分取ってグラフ化してます。おおよそ精度は0.01以内です。\(h\)の刻みをより細かくすればもっと精度が良くなると思いますが、今回は比較なのでこれくらいにしてきます。
中心差分
続いて中心差分を見てみます。
\begin{align} f^{\prime}(x)\approx\frac{f(x+h)-f(x-h)}{2h} \end{align}xの前方、後方の点から近似します。同様に精度を見てみます。
▼精度確認(中心差分)▼
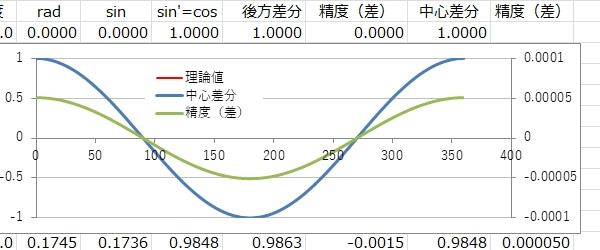
精度はおよそ、0.00005以内、めちゃめちゃ良くなりました。200倍ほど、、こんなに違う。精度の解像度?分布?も後方差分と違います。
リアルタイムな解析では中心差分は使いにくそうですが、こんなに精度差がでるなら使えるときは使っていきたいですね。

コメント