ジャイロ（角速度）から角度の算出方法

　ジャイロ検出値（角速度）から角度の計算方法と、その精度、について触れてみたいと思います。ジャイロスコープ（センサー）から取得できる値は角速度が一般的かと思います。中には角加速度が取得されるものもありますが、ここでは角速度が取得できるものを前提とします。

角速度とは

　角速度とは単位時間当たりに回転した角度です。例えば、1秒後に30度の角度であれば角速度は30deg/sで、10秒後に50度の角度であれば5deg/sとなります。いわゆる回転する速度のことをいいます。角度の単位は度（deg）、ラジアン(rad)の場合があります。

　センサーによっては角速度の取得値を電圧で返すものがあります。センサーのデータシートに感度と記載があり、単位がmv/deg/sなどと記載されているものです。これは単位時間当たり1度（deg）の変化に対する出力電圧です。

　仮にデータシートに0.67mv/deg/sと記載があるセンサーを使う場合、センサーから検出された電圧差を50mvとすると、角速度は50÷0.67≒74.6deg/sとなります。

　角速度から角度への計算方法ですが、センサーから取得される角速度を積分すると角度となります。積分というと難しい感じがしますが、ようは面積です。

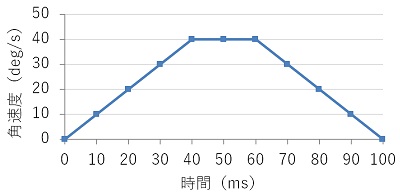
　10ms毎のセンサーの取得値（角速度）が上のグラフであった場合、グラフで囲まれた面積が角度となります。

　例えば、40ms（0.04s）後の角度は三角形部分の面積となるので、

\begin{align} \\ \frac{0.04s\times 40deg/s}{2}=0.8deg \\\\ \end{align}

となります。

　また、例えば、100ms後の角度は全体の面積（台形部分）となるので、

\begin{align} \\ \frac{\left(0.04s+0.1s\right)\times40deg/s}{2}=2.4deg \\\\ \end{align}

となります。

　角速度からの角度算出をプログラム言語で表現する方法です。2通りの計算方法とその違いを紹介します。

　1つ目は単純に積算していく方法です▼

while(1) {
  degree += gx * dt;
}

　よく目にする記述かと思います。角速度(gx)に時間（角速度を検出する間隔）（dt）を掛けて足し続ける方法です。

　先ほどのグラフで表現すると
　
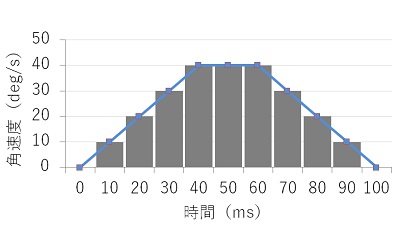
　長方形の面積を足していく感じです。斜めの部分があるため、多少の誤差は発生します。ただ実際には、角速度を検出する時間間隔を非常に小さく設定すると思います。そのため、誤差も無視しても問題ないくらい小さいものになると思います。

　長方形の面積を足していくと、40ms後の角度は1.0degとなり、先ほどの面積計算（0.8deg）と誤差が生じてます。（今回の例では最終100ms後の角度誤差はなくなります）

　2つ目は台形の面積で積算していく方法です▼

while(1) {
  degree += (pregx + gx) * dt / 2;
  pregx = gx;
}

▲gxが取得した角速度値、pregxが一つ前の角速度値です。

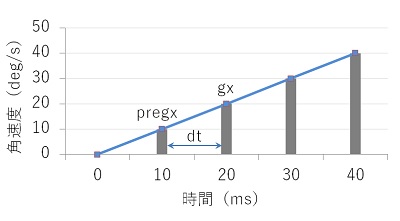
　2つの角速度値から面積を台形で計算し、積算していく方法です。この方法ですと長方形の積算よりも誤差が小さくてすみます。

　紹介したどちらの方法でも角速度から角度の算出は可能です。ただセンサーには個体差や温度、周辺からの影響などでノイズが含まれます。値を積算していく際に、これらのノイズも積算していくため、角度算出値に誤差が積みあがっていきます（ジャイロドリフト）。このドリフトについては別途補正してやる必要があります。

　またここではあまり触れませんでしたが、1軸回転だけではなく、3軸回転があるような場合は、センサー座標系が回転してしまうため、単純な積算ではなく、回転行列や四元数（クォーターニオン）などでベクトルを合わせて角度を算出する必要があります。

▼単純な積算▼

　一番右側の姿勢計算はジャイロ値を1軸ずつ単純に積算しているだけです。最終的にはベクトルそのものがずれてしまってます。3次元で姿勢角度を推定するときにはベクトルを考慮して計算する必要があります。